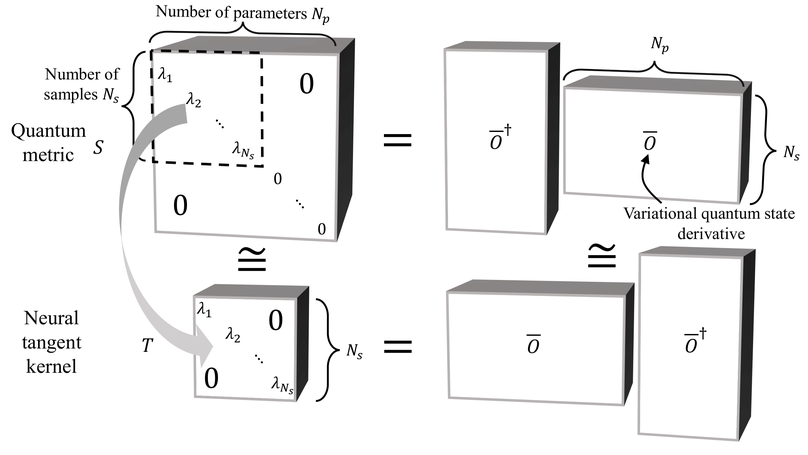
Computing the ground state of interacting quantum matter is a long-standing challenge, especially for complex two-dimensional systems. Recent developments have highlighted the potential of neural quantum states to solve the quantum many-body problem by encoding the many-body wavefunction into artificial neural networks. However, this method has faced the critical limitation that existing optimization algorithms are not suitable for training modern large-scale deep network architectures. Here, we introduce a minimum-step stochastic-reconfiguration optimization algorithm, which allows us to train deep neural quantum states with up to 10^6 parameters. We demonstrate our method for paradigmatic frustrated spin-1/2 models on square and triangular lattices, for which our trained deep networks approach machine precision and yield improved variational energies compared to existing results. Equipped with our optimization algorithm, we find numerical evidence for gapless quantum-spin-liquid phases in the considered models, an open question to date. We present a method that captures the emergent complexity in quantum many-body problems through the expressive power of large-scale artificial neural networks.

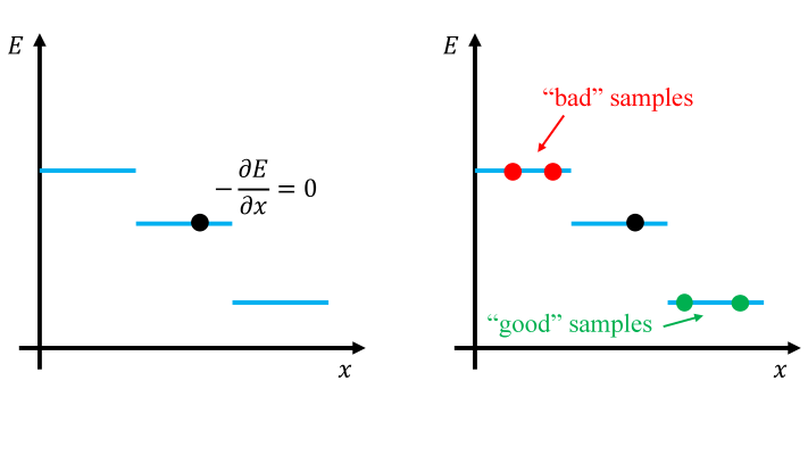
Feed-forward neural networks are a novel class of variational wave functions for correlated many-body quantum systems. Here, we propose a specific neural network ansatz suitable for systems with real-valued wave functions. Its characteristic is to encode the all-important rugged sign structure of a quantum wave function in a convolutional neural network with discrete output. Its training is achieved through an evolutionary algorithm. We test our variational ansatz and training strategy on two spin-1/2 Heisenberg models, one on the two-dimensional square lattice and one on the three-dimensional pyrochlore lattice. In the former, our ansatz converges with high accuracy to the analytically known sign structures of ordered phases. In the latter, where such sign structures are a priory unknown, we obtain better variational energies than with other neural network states. Our results demonstrate the utility of discrete neural networks to solve quantum many-body problems.