Neural Network Evolution Strategy for Solving Quantum Sign Structures

Abstract

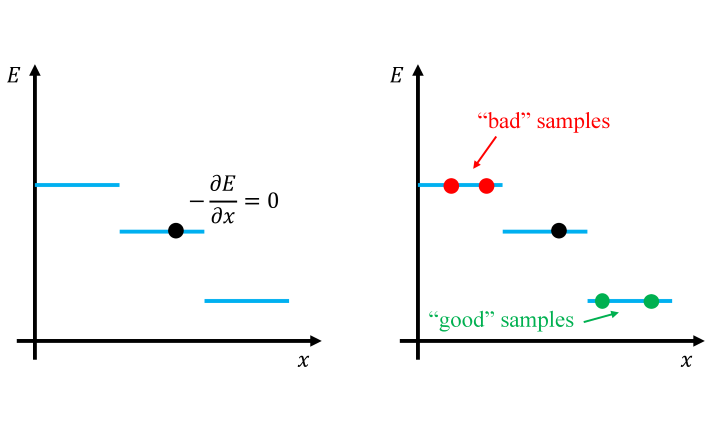
Feed-forward neural networks are a novel class of variational wave functions for correlated many-body quantum systems. Here, we propose a specific neural network ansatz suitable for systems with real-valued wave functions. Its characteristic is to encode the all-important rugged sign structure of a quantum wave function in a convolutional neural network with discrete output. Its training is achieved through an evolutionary algorithm. We test our variational ansatz and training strategy on two spin-1/2 Heisenberg models, one on the two-dimensional square lattice and one on the three-dimensional pyrochlore lattice. In the former, our ansatz converges with high accuracy to the analytically known sign structures of ordered phases. In the latter, where such sign structures are a priory unknown, we obtain better variational energies than with other neural network states. Our results demonstrate the utility of discrete neural networks to solve quantum many-body problems.